前言
这篇文章讲了啥?
- 链表判断环
- 链表判断入口点
- 快慢指针是否一定能相遇
一、怎么判断链表是否有环?
- 快慢指针的方式(快指针一次走两步,慢指针一次走一步)
- 循环查重
二、为什么快慢指针一定能相遇(在快步长是 2,慢步长是 1 的情况下)?
由于链表是个环,所以相遇的过程可以看作是快指针从后边追赶慢指针的过程
当快慢指针相差一步的时候,继续往后走,慢指针走一步,快指针走两步,两者相遇
当快慢指针相差两步的时候,继续往后走,慢指针走一步,快指针走两步,那么此时两者相差一步,转换为第一种情况
当快慢指针相差 N 步的时候,继续往后走,慢指针走一步,快指针走两步,那么此时两者相差 N-1+2=N-1 步,由于 N 是逐渐变小的,所以最终快慢指针一定能相遇
三、为什么快指针一次走一步,慢指针一次走两步,走 3 步 4 步可不可以?2 步 6 步可不可以?
先说答案可以
设:两格指针步长是 a,b,步数是 x,环的长度是 L,则
1 | ax ≡ bx (mod L) |
表示 ax 与 bx 对模 L 同余, 这啥意思呢?翻译成 js 就是这样的 ax%L = bx%L ,就是俩余数相等
也就是当这个等式成立的时候,快慢指针才能相遇,变换一下
1 | ax-bx ≡ 0(mod L) === > x(a-b) ≡ 0(mod L) |
根据这个等式可以得出一下结论
那么当x=0的时候,等式成立,快慢指针相遇,x=0是最小值当x(a-b) (mod L) = 0等式成立
x=0 的时候就是一步还没走,关键是第二个等式的成立条件
x(a-b) 必须是 L 的整数倍
那么能得出结论,判断快慢指针是否能相遇,则必须满足这个条件x(a-b) (mod L) = 0
进而可以知道,快慢指针相遇的关键因素就是差值、环长、步数,再次简化,当 x 是 L 的倍数的时候无论 a,b 取值为多少,都能相遇
先说下为啥一般快慢指针步长都是 1 和 2,就是因为好算
回到这个问题
| 快 | 慢 | 判断方法,x(步长),L(环长) | 结论 |
|---|---|---|---|
| 4 | 3 | 4-3=1,则只需要满足 x(mod L)=0 即可相遇 | 当 x 是 L 整数倍一定可以相遇 |
| 6 | 2 | 6-2=4,则只需要满足 4x(mod L)=0 即可相遇 | 当 x 是 L 整数倍一定相遇 |
结论
- 快慢指针相遇的关键因素就是环长、步数,当步数是环长的整数倍,则一定能相遇
- 快慢指针无论取什么值,知道 x(步数)是 L(环长)的整数倍,则一定能相遇
- 判断快慢指针是否能相遇的公式x(a-b) (mod L) = 0
四、怎么找到入口节点
第一种方法,一把梭,直接循环遇到的第一个重复节点就是入口点
第二种,快慢指针
为啥快慢指针能找到入口点,我先用 ps 画个图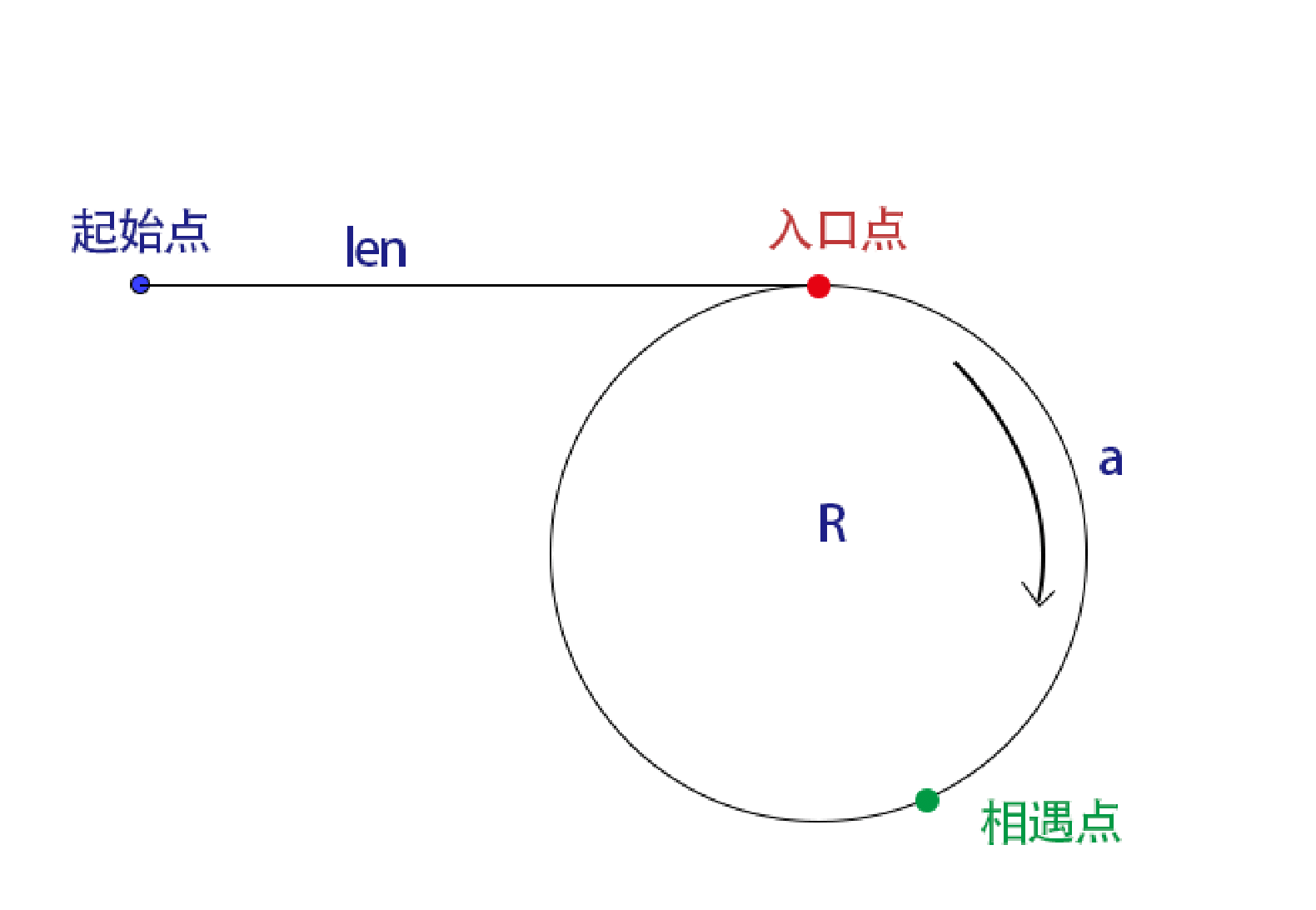
设起始点到入口点距离是 len
入口点到相遇点距离是 a
环长是 R
快指针在环里走了几圈 n
则快指针走过的距离为:len+nR+a
慢指针走过的距离:len+a
则有如下关系
len+nR+a=2(len+a)==>len=nR-a(n>=1)
当 n=1 的时候,len=R-a
所以首先找到相遇点,然后继续往下走,从起始点也同步往下走,当相遇时则就是入口点
